SOAL OLIMPIADE SAINS NASIONAL 2025 DAN ALTERNATIF PENYELESAIANNYA (TINGKAT KOTA/KABUPATEN PART C)
Dalam suatu lingkaran berpusat di O berjari-jari 7, dibuat segitiga ABC dengan titik A, B, dan C terletak pada lingkaran, AC merupakan diameter lingkaran dan ∠ACB = 60°.
Melalui C dan titik tengah AB, dibuat garis memotong lingkaran di titik D. Ukuran panjang CD sama dengan .…
A. 3√7
B. 5√7
C. 6√7
D. 7√7
Alternatif Penyelesaian:
Perhatikan gambar berikut.
Lingkaran O berjari-jari 7. Karena AC diameter, akibatnya sudut B siku-siku. Dengan perbandingan sisi-sisi segitiga istimewa 60°, 90°, dan 30°, akibatnya AC = 14, BC = 7, dan AB = 7√3. Misalkan X adalah titik tengah AB,
AX = XB = AB : 2
⇔ AX = XB = 7√3 : 2
Dengan rumus Pythagoras, diperoleh
CX² = BC² + XB²
CX ∙ XD = AX ∙ XB
CD = CX + XD
⇔ CD = 5√7
(Pilihan jawaban B benar).




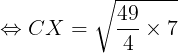

Posting Komentar untuk "SOAL OLIMPIADE SAINS NASIONAL 2025 DAN ALTERNATIF PENYELESAIANNYA (TINGKAT KOTA/KABUPATEN PART C)"
Posting Komentar